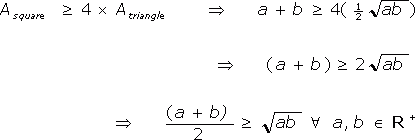Introduction

This is a fairly random proof of a simple special case of the arithmetic/geometric mean inequality (which is basically that the sum of a set of n positive real numbers, divided by n, is at least as large as the nth root of the product of the same n positive real numbers). It's not a very useful proof, because it doesn't add anything to your understanding of the problem and can't be extended to more than 2 numbers, but it has weird looking diagrams :-)

Geometric proof that (a+b)÷2 ≥ √ab (a, b ∈ R+)

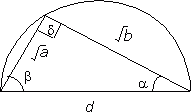The same diagram with some sides labelled Fig.1

Consider a triangle inscribed in a semicircle as shown (Fig.1), with its longest side the semicircle's diameter d, and its shorter sides √a and √b. Let the angles adjacent to this side be α and β. The angle opposite the diameter, d, is 90°, because the angle subtended at the circumference is half the angle subtended at the centre (in this case, 180°). This implies that α+β=90°. Also, by Pythagoras' Theorem (as d is a right angle),

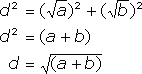
d squared = (sqrt(a)) squared + (sqrt(b)) squared; d squared = a + b; d = sqrt(a+b)

The area of the triangle is ½ × base × perpendicular height and, as d is a right angle, Atriangle = ½ √a√b = ½ √(ab).

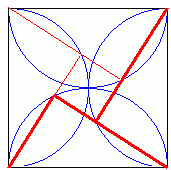Four semicircle/triangle sets with the hypotenuses forming the sides of a square, and everything else inside that square; the bottom and right triangles are emphasised with thicker lines Fig.2

Consider four of these arrangements, placed together as shown (Fig.2), such that the hypotenuses of the triangles form a square of side d=√(a+b), which therefore has area (a+b). The triangles touch but do not overlap at each side, as α+β=90°. This means that, in any pair of adjacent triangles (one such pair is shown with thicker lines in Fig.2), the triangles do not overlap at any point.

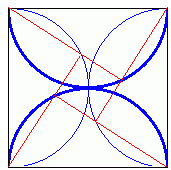Same as Fig.2, but this time the top and bottom semicircles are emphasised Fig.3

As the square has height and width d=2 radii, the semicircles in which opposite triangles are inscribed (highlighted in Fig.3) touch at the centre (i.e. have a common tangent) but do not overlap. The triangles lie entirely within these semicircles and therefore cannot overlap either, although they will touch at the centre of the square when α=β=45°.

As there is no overlap between any triangles in this arrangement,

A(square) is at least 4A(triangle), so a+b is at least 4 x 1/2 x sqrt(ab), so (a+b)/2 is at least sqrt(ab) for all positive real a, b. QED.